转动惯量那点事
缘起
转动惯量有一个非常重要而有趣的性质,很容易叙述,也很容易应用,它是上述分析的基础,但它太复杂,难于在这里证明。这个性质叙述如下:任何刚体,即时是像马铃薯之类不规则的物体,都有通过质心的三根相互垂直的轴,使得相对于这三根轴中某一根轴的转动惯量与通过质心的任何轴相比具有最大可能值;相对于这三根轴中另一根轴的转动惯量则具有最小可能值;而对于第三根轴的转动惯量则处于两者之间(或等于其中之一).这三根轴称为物体的主轴,它们具有一个很重要的性质——如果物体绕其中一个轴转动,它的角动量与角速度的方向相同。对于具有对称轴的物体来说,它的主轴就是对称轴。
也就是说,过刚体质心存在相互垂直的最大转动惯量轴和最小转动惯量轴!对我们这些小白来说,这是这段话中最新最深的一层含义了。
为什么?

然后……
本来没觉得是个大case。就随口问了一下在科大读物理的原。然后他发给了我一堆不明觉厉的东西……



浙大学渣已被虐哭……我终于见识了科大理科生的可怕!!!
原以为分析落远了,代数知识范围还是可以完爆他的。后来发现自己实在naive,科大的线性代数第一章……呃……可怕。真是不敢想讲个线性空间就要在前面铺垫海森阵这种我连听都没听说过的东西……
弃理从工逃逃逃……
不过原的推导最后进了死胡同。看来费恩曼老人家说的“它太复杂,难于在这里证明”不是说着玩的。原写的都是求和形式,不过最后他想知道的那个求和……即便在我很low的数学看来,也不觉那是个级数,应该是个黎曼和。
那么为什么不用积分的语言呢?
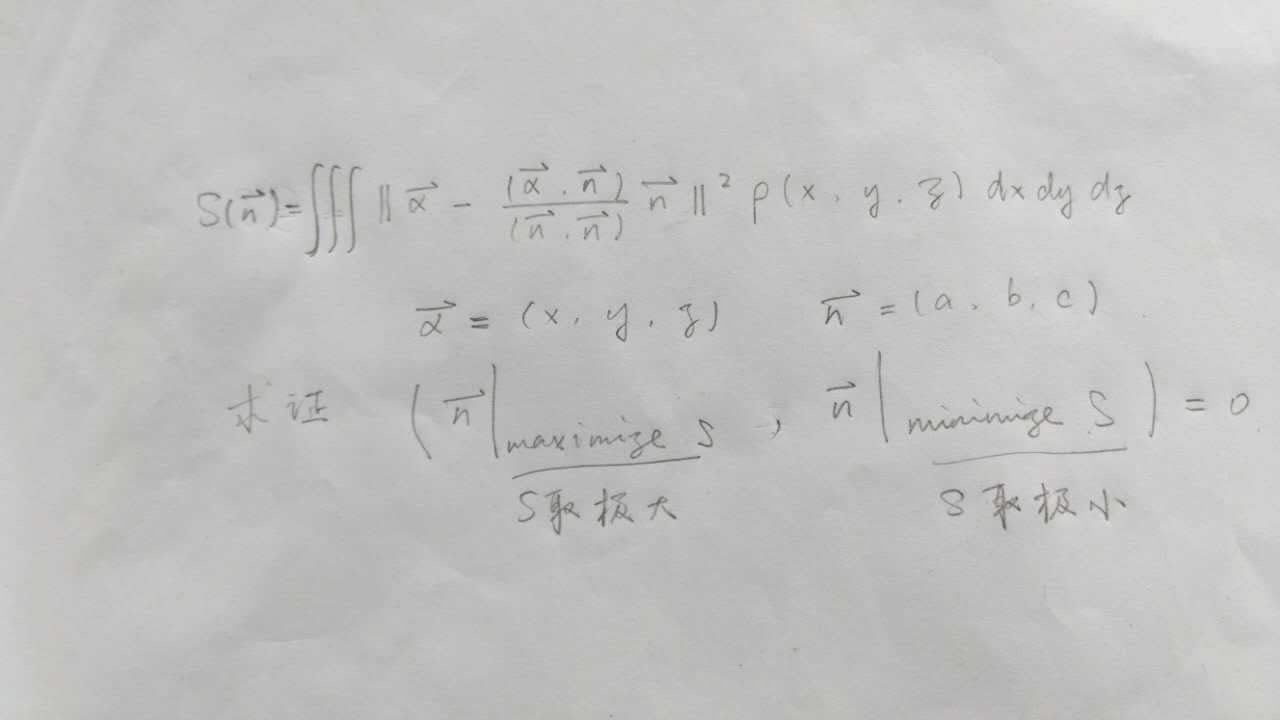
翻译成数学就是这样了。
然后……我想到了Mathematica。
1 | Clear["Global`*"] |
我以为应该是对的了吧。Shift + Enter之后,Out豁然为0!我欣喜若狂,以为万能的Mathematica完成了一系列推导,最终约得答案为0!我还Trace了一下,并深信不疑,仔细分析Trace就能得到推导过程。

原最开始也深信不疑。不过看出来科大学生不虚那扎实学风了。他自己亲身实践了一下,发现了问题。我看了他发的代码和输出截图一下子感觉大事不妙。交流之后我真是又有想跪的心了——我刚把Mathematica推荐给他,这哥们以前就用过WolframAlpha,才一天他就能挑bug了。啊啊啊,两年的Mathematica白玩了(←_←本来你也没好好学过Mathematica)。
替换乱掉了,替换乱掉了,替换乱掉了!
可以推(xi)倒(xi)重(shui)来(le)。
我也不知道自己是真抽不出时间还是在搪塞我的好哥们,等我晚上看看,等我晚上用电脑看看……然而晚上在查中山舰事件的资料……
今天感觉浑浑噩噩了一天,哎呀,写完就睡。下午愣是在寝室鼓捣出来另一个打法:
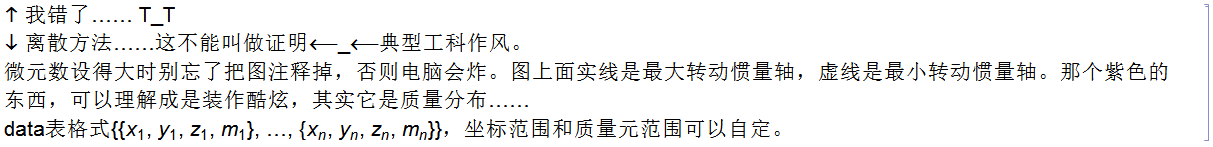

嗯,也就是说我要生成随机刚体(其实就是一群质点),通过具体问题具体分析,验证一下。
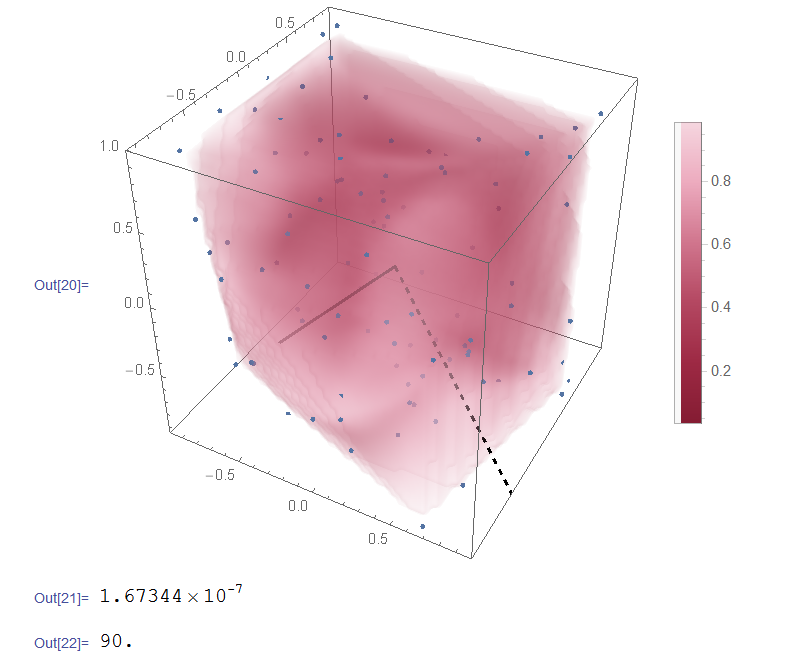
是不是很酷?感觉很高端的样子(实际上没什么大用)。图中的散点即为随即生成的质点,紫色半透明区域是密度分布啦。实粗线是转动惯量最大轴矢量,虚粗线是转动惯量最小轴矢量。下面计算结果可以看出,在有计算误差的情况下,它们的内积已经很接近0,成角为90°。
我发给原代码,原还没回我。
睡啦睡啦……
欸,有没有发现忽视了“过质心”这一条件,难道说……